Cómo resolver un ejercicio de MRU

En este post vamos a hacer un recorrido por el Movimiento Rectilíneo Uniforme o MRU, desde qué significa, pasando por las condiciones en las que se puede aplicar, hasta un ejercicio resuelto en el que podremos fijarnos como base para resolver más.

¿Qué es un MRU?

MRU son las siglas de movimiento rectilíneo uniforme. Analicemos cada una de las palabras de este nombre:

Movimiento, dado que tiene que existir un cambio en la posición del objeto que vamos a estudiar(a partir de ahora lo llamaremos móvil).

Rectilíneo dado que su trayectoria es recta y durante su recorrido no se producen cambios de sentido.

Uniforme porque la velocidad es constante, es decir, en todo el movimiento la velocidad es la misma.

Ecuación del movimiento.

La ecuación del movimiento es una función que relaciona la posición del móvil con el tiempo transcurrido. Si lo traducimos a un lenguaje más cercano, es una fórmula que nos dice a que distancia del comienzo está un objeto cuando ha pasado un cierto tiempo.

En esta ecuación aparecen una serie de símbolos que es necesario definir:

[latex]x[/latex]: es la posición, es decir, la distancia a la que está de nuestro punto de referencia. Se puede sustituir por [latex]s[/latex]. [ [latex]m[/latex] ] [latex]x_o[/latex]: es la posición inicial, es decir, la distancia a la que se encuentra el móvil de nuestro punto de referencia en el momento en el que comienza el movimiento. Se puede sustituir por [latex]s_o[/latex]. [ [latex]m[/latex] ] [latex]v[/latex]: es la velocidad. Si el objeto se acerca al punto de referencia tendrá signo negativo y si se aleja tendrá signo positivo. [ [latex]m/s[/latex] ] [latex]t[/latex]: es el tiempo. [ [latex]s[/latex] ]

Una vez que hemos definido todas las posibles variables, podemos escribir la ecuación del movimiento:

[latex]x=x_o+vt[/latex]

Es importante saber que en la ecuación del movimiento las incógnitas son [latex]x[/latex] y [latex]t[/latex], es decir, que si nos piden que escribamos la ecuación del movimiento, tenemos que sustituir los valores de [latex]v[/latex] y [latex]x_o[/latex].

Vamos a ver un ejemplo: Un objeto se encuentra a 2m de nuestro cuerpo, cuando empieza a moverse con una velocidad constante de 30m/s. Escribe la ecuación del movimiento de este MRU:

Lo primero para resolver el ejercicio sería asegurarse de que movimiento se trata (en nuestro caso es un MRU porque nos dicen que la velocidad es constante y al final que es un MRU). En segundo lugar, tenemos que apuntar los datos indicando que son ([latex]x_o=2m[/latex] y [latex]v=30m/s[/latex]). Por último escribimos los datos sin sustituir ni x ni t. De esta forma, la ecuación del movimiento sería:

[latex]x=2m+30m/s\cdot t[/latex]

Ecuación de la velocidad.

La ecuación de la velocidad es una fórmula que nos relaciona la velocidad con el espacio y el tiempo. A partir de esta podemos obtener el valor de la velocidad en un MRU.

[latex]v=\frac{x-x_o}{t-t_o}[/latex]

Veamos un ejemplo: Un coche recorre 3km en 4 minutos. ¿Cuál es la velocidad del coche?

Datos: [latex]x-x_o=3km=3000m[/latex]

    [latex]t-t_o=4min=240s[/latex]

Operación: [latex]v=\frac{3000m}{240s}=12m/s[/latex]

Gráficas posición-tiempo y velocidad-tiempo.

La representación gráfica de estas ecuaciones es muy simple. La ecuación de movimiento es una función lineal, es decir, una recta inclinada. Le ecuación de la velocidad es una función constante, es decir, una recta horizontal.

Para representar la gráfica posición tiempo hacemos una tabla de valores y unimos estos valores con una recta.

Para representar la gráfica velocidad-tiempo hacemos una recta horizontal del tipo [latex]y=v[/latex]. De esta gráfica podemos obtener el desplazamiento si hacemos el área del rectángulo que existe entre dos tiempos.

Veamos un ejemplo: Represente la gráfica posición-tiempo y velocidad-tiempo de un movimiento definido mediante la siguiente ecuación del movimiento [latex]x=3m+2m/s \cdot t[/latex] y calcule el desplazamiento en 30s a partir de la gráfica velocidad-tiempo.

Tabla de valores:

[latex]\begin{matrix}x(m)&t(s)\\3 & 0\\5 & 1\\7&2\end{matrix}[/latex]

Esto hace que la gráfica posición-tiempo sea del tipo: 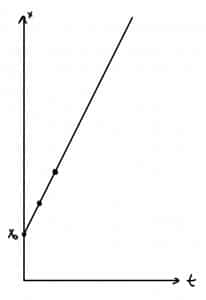Para representar la gráfica velocidad-tiempo hacemos una recta horizontal del tipo [latex]y=v[/latex]:

Para calcular el desplazamiento entre t=0 y t=30 tenemos que calcular el área del rectángulo que sale al cortar la gráfica por esos dos tiempos. La base mediría 30 y la altura es la velocidad, es decir, 2.

Cálculo: [latex]A_{r}=b \cdot h=30 \cdot 2=60[/latex]

Esto implica que el desplazamiento en 30s es de 60m. Este desplazamiento no coincide con la posición porque el desplazamiento es [latex]\Delta x=x-x_o[/latex]

Cruces, encuentros y persecuciones.

Un cruce, un encuentro y una persecución implican la misma condición física: la posición de los móviles estudiados es la misma.

Para explicarlo vamos a poner un ejemplo: Madrid y Valencia están separados por 300km. Un coche sale de Madrid hacia Valencia con una velocidad constante de 90km/h, mientras otro sale de Valencia hacia Madrid con una velocidad constante de 126km/h. Calcula a que distancia de Madrid se encontrarán los coches.

Primero tenemos que escribir los datos en sus unidades del sistema internacional.

Datos:

Distancia Madrid-Valencia: 300000m

Velocidad coche de Madrid: [latex]90km/h \frac{1000m}{1km}\frac{1h}{3600s}=20m/s[/latex]

Velocidad coche de Valencia: [latex]-126km/h \frac{1000m}{1km}\frac{1h}{3600s}=-35m/s[/latex]

Establecemos nuestro sistema de referencia. En mi caso lo voy a colocar en Madrid dado que nos piden la distancia a Madrid.

Hallamos las ecuaciones de los dos móviles teniendo en cuenta el sistema de referencia elegido. La velocidad del coche de Valencia será negativa porque se acerca a nuestro punto de referencia que es Madrid.

[latex]x_M=0m+20m/s\cdot t[/latex] [latex]x_V=300000m-35m/s\cdot t[/latex]

La condición física de encontrarse o cruzarse es [latex]x_M=x_V[/latex] y la aplicamos para resolver la ecuación (obtener el timepo que tardan en encontrarse).

[latex]20m/s\cdot t=300000m-35m/s\cdot t[/latex] [latex]35m/s\cdot t+20m/s\cdot t=300000m[/latex] [latex]55m/s\cdot t=300000m[/latex] [latex]t=\frac{300000m}{55m/s}=5454’55s[/latex]

Una vez que hemos calculado el tiempo que tardan en encontrarse, introducimos este dato en cualquiera de las dos ecuaciones del movimiento para obtener la distancia a Madrid

[latex]x_M=0m+20m/s\cdot 5454’55s = 109091 m [/latex] [latex]x_V=300000m-35m/s\cdot 5454’55s = 109090’75 m [/latex]

El motivo de que no salga exactamente el mismo número es la aproximación. La respuesta sería: La distancia de Madrid a la que se encuentran los dos coches es 109091m, es decir, 109’1km.