Cómo hacer la representación gráfica de una función

En este post vamos a tratar de explicar los pasos necesarios para poder hacer la representación gráfica de una función. Bien es sabido por todos los estudiantes que las funciones están presentes en nuestro recorrido académico, tanto si vamos por ciencias como por ciencias sociales. Desde que en los primeros cursos de la ESO nos explican cómo representar puntos en los ejes coordenados, las funciones van complicándose más y más, hasta que en Bachillerato ya nos piden hacer un estudio exhaustivo de las mismas.

Lo primero que tenemos que tener en cuenta al hacer el estudio de una función es su dominio. Si es una función racional, nos fijaremos en los valores que anulan su denominador; si es logarítmica, su argumento (lo que está dentro del logaritmo) tiene que ser mayor que cero; si es radical, lo que se encuentra bajo el signo radical tiene que ser mayor o igual que cero; si es polinómica, en cambio, su dominio serán todos los números reales. Es decir, tenemos que conocer bien los tipos de funciones y qué dificultades nos puede presentar cada una.

Después, analizaremos los puntos de corte con los ejes coordenados, igualando x e y a cero. Podemos también (aunque generalmente no será necesario) estudiar el signo de la función: a partir del valor o los valores que hagan que y valga cero, podemos ver si números que se encuentran antes o después nos dan un valor positivo o negativo en la función. El estudio de la paridad también es opcional siguiendo el criterio:

[latex]\begin{cases}\textrm{Si }f(x)=f(-x)\Rightarrow\textrm{funci\’on par}\\\textrm{Si }f(x)=-f(-x)\Rightarrow\textrm{funci\’on impar} \end{cases}[/latex]

Tras esto, podemos estudiar las asíntotas de la función. Recordad que en las funciones racionales serán aquellos puntos que anulen el denominador (es decir, los que estén excluidos del dominio); tendremos que ver qué sucede a la izquierda y a la derecha de dichos puntos para ver cómo se comporta la función. Después, veremos qué sucede con las asíntotas horizontales, haciendo el límite cuando [latex]x\rightarrow\pm\infty[/latex], y recordad que si hay asíntota horizontal, no hay oblicua: esta solo existirá cuando tengamos una función racional y el grado del numerador sea una unidad mayor que el del denominador.

Posteriormente, derivaremos la función e igualaremos a cero para ver los candidatos a extremos relativos. Recordad este criterio:

[latex]\begin{cases}\textrm{Si }f'(a)=0\textrm{ y }f”(a)<0\Rightarrow a\textrm{ es un m\’aximo}\\\textrm{Si }f'(a)=0\textrm{ y }f”(a)>0\Rightarrow a\textrm{ es un m\’inimo} \end{cases}[/latex]

Obtenidos los extremos relativos, y junto con las asíntotas verticales que podamos tener, estudiamos el signo de la primera derivada a la izquierda y a la derecha de dichos puntos para ver la monotonía: si es positiva, la función será creciente; si es negativa, decreciente.

En los puntos en los que se anule la segunda derivada tendremos puntos de inflexión, que junto con las asíntotas verticales nuevamente nos servirán para estudiar la curvatura de la función:

[latex]\begin{cases}\textrm{Si }f”(x)>0\Rightarrow \textrm{funci\’on c\’oncava}\\\textrm{Si }f”(x)<0\Rightarrow \textrm{funci\’on convexa} \end{cases}[/latex]

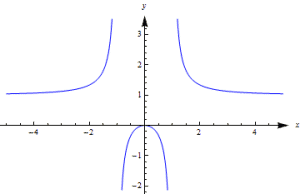
Para concluir, os dejamos, a modo de ejemplo, la representación gráfica de una función racional, analizando todos los pasos que hemos comentado en el texto.